선형 독립성
부분공간(subspace)
기저(basis)
영벡터
모든 성분이 0인 벡터
벡터 집합
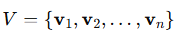
선형 가중 결합(linear weighted combination)
벡터 집합에서 벡터의 차원이 같을 때
각 벡터의 차원에 스칼라를 곱한 다음 합해 하나의 벡터를 만드는 것

w는 선형 결합으로 생성된 벡터
c1, c2, ..., cn은 각 벡터에 곱해지는 스칼라
선형 독립성
벡터 집합에서 적어도 하나의 벡터가
집합 내의 다른 벡터들의 선형 가중 결합으로 나타낼 수 있을 때 벡터 집합은 선형 종속적
집합 내의 다른 벡터들의 선형 가중 결합으로 나타낼 수 없을 때 벡터 집합은 선형 독립적


선형 종속적이라면

이 공식을 바꾸면
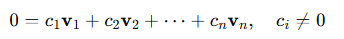
적어도 하나의 스칼라값이 0이 아닐 때 (적어도 하나의 c =/= 0)
선형 종속적이면 벡터들의 선형 가중 결합으로 영벡터를 만들 수 있다.
선형 독립적이면 벡터들의 선형 가중 결합으로 영벡터를 만들 수 없다.
+ 영벡터가 포함된 모든 벡터 집합은 선형 종속적

공식을 이용하면 벡터 집합 내에 영벡터가 포함되어 있을 때

적어도 하나의 스칼라 값(영벡터의 스칼라 값)이 0이 아닌 값을 가질 수 있기 때문에 선형 종속적이다
-> 벡터 집합 내에 영벡터가 포함된다면 그 벡터 집합은 선형 종속적
부분공간(subspace)과 생성(span)
부분공간: 벡터 집합 안에서 벡터들의 선형 결합으로 만들 수 있는 모든 벡터들이 포함된 공간
벡터 부분공간 만드는 법: 동일한 벡터를 사용하면서, 가중치를 다르게 선택하여 무한히 선형 결합하는 방식
벡터집합의 생성: 가능한 모든 선형 가중 결합을 구성하는 메커니즘
모든 가중치를 0으로 설정했을 때 만들어지는 영벡터도 부분공간에 존재
부분공간 안에 있는 벡터들의 선형 가중 결합으로 만들어지는 벡터도 부분공간에 존재
생성 부분공간의 차원과 벡터 수의 관계: 부분공간의 차원은 선형 독립 집합을 형성하는 데 필요한 최소한의 벡터 수
선형 독립적
부분공간의 차원 = 벡터 수
선형 종속적
부분공간의 차원 < 벡터 수
기저(basis)
벡터 공간을 구성하는 최소한의 벡터 집합
해당 벡터 공간의 모든 벡터를 선형 결합으로 표현할 수 있도록 해주는 독립적인 벡터들의 집합
벡터 집합이 특정 부분공간을 생성하고 선형 독립적이라면 그 집합은 해당 부분공간의 기저
데카르트 기저 집합
서로 직교하며, 단위 길이인 벡터로 이루어짐
2차원 데카르트 기저 집합: {[1,0],[0,1]}
3차원 데카르트 기저 집합: {[1,0,0],[0,1,0],[0,0,1]}
같은 부분공간이라고 해도, 그 부분공간을 표현하는 기저는 다를 수 있다
-> 어떤 부분공간에 대한 최적의 기저벡터 집합을 찾는 것이 중요
'혼자 공부 > 선형대수학' 카테고리의 다른 글
| 행렬의 연산, 행렬 곱의 전치 증명, 대칭 행렬 (0) | 2025.04.19 |
|---|---|
| 행렬1 (0) | 2025.04.17 |
| 상관관계와 코사인 유사도 (0) | 2025.03.18 |
| 직교벡터 분해 (0) | 2025.03.05 |
| 벡터1 (0) | 2025.03.03 |