개발자를 위한 실전 선형대수학(파이썬 3.10 버전 대응, 구글 코랩 실습 가능) | 마이크 X 코헨 - 교
개발자를 위한 실전 선형대수학(파이썬 3.10 버전 대응, 구글 코랩 실습 가능) | 복잡한 증명과 수식 없이 파이썬을 이용해 직관적으로 배우는 선형대수학 * 연습문제 + 해답 + 해설 강의, 무료 샘
product.kyobobook.co.kr
스칼라
크기만 가지고 방향이 없는 값
벡터
크기와 방향을 모두 가지며, 순서대로 나열된 수의 목록
Numpy 라이브러리 임포트
import numpy as np
벡터 생성
arr = np.array([1,2,3]) # 1차원 배열(방향이 없음)
row_vec = np.array([ [1,2,3] ]) # 행 벡터
col_vec = np.array([ [1],[2],[3] ]) # 열 벡터
벡터의 차원(행렬의 차원)

벡터의 덧셈, 뺄셈, 곱셈(아다마르곱)
대응대는 원소끼리 연산
차원이 일치해야 한다
# 리스트
a = [1,2,3]
b = [4,5,6]
print(a + b) # 리스트 연결
print(np.array(a) + np.array(b)) # 벡터의 덧셈
스칼라-벡터 곱셈
각 벡터의 원소에 스칼라 값을 곱한다
a = [1,2,3] # 리스트
s = 2 # 스칼라
print(a * s) # 리스트 반복
print(np.array(a) * s) # 스칼라-벡터 곱셈
넘파이에서의 스칼라-벡터 덧셈
브로드캐스팅을 통해
a = [1,2,3] # 리스트
s = 2 # 스칼라
print(np.array(a) + s) # 스칼라-벡터 덧셈 [1, 2, 3] # 1차원 배열
+ [2, 2, 2] # 브로드캐스팅
-------------
[3, 4, 5] # 결과
벡터의 전치 연산(transpose)
열벡터 <-> 행벡터
벡터를 두 번 전치하면 다시 자기 자신이 된다.

row_vec = np.array([ [1,2,3] ])
col_vec = np.array([ [1,2,3] ]).T # 전치
# np.transpose( np.array([ [1,2,3] ]) )와 같음
row_vec, col_vec
열벡터 만들 때 대괄호의 수를 줄이기 위해 먼저 행벡터로 만든 다음 전치하여 열벡터로 변환한다
벡터 노름
벡터의 노름 = 벡터의 크기
유클리드 거리 공식(벡터 원소들의 제곱합에 제곱근)을 통해 구한다

# 벡터의 노름 구하기
v = np.array([ [1,2,3] ])
print(np.linalg.norm(v))
print(np.sqrt(np.sum(v**2))) # 제곱해서 더한 것에 제곱근을 취함
단위벡터(Unit vector)
노름이 1인 벡터

단위벡터 만드는 법
벡터에 벡터 노름의 역수(스칼라)를 곱한다


# 단위벡터 구하기
v = np.array([1,2,3])
norm = np.linalg.norm(v)
u = v/norm
u
벡터-내적
내적(dot product): 두 벡터 사이의 관계를 숫자로 나타내는 것
차원이 일치해야 한다
1. 대수적 정의
두 벡터에 대응되는 원소끼리 곱한 다음 합한다
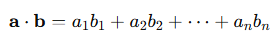
전치 연산을 이용한 내적 공식
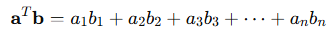
자기 자신 내적하면 노름의 제곱이 된다
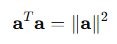

a = np.array([1,2,3,4])
b = np.array([5,6,7,8])
print(np.dot(a,b))
print(np.sum(a*b))
2. 기하학적 정의
a의 b로의 정사영의 길이에 b의 크기를 곱한 것
(=벡터 a의 변화를 벡터 b가 얼만큼 설명해줄 수 있는가)
자기 자신을 내적하면 노름의 제곱
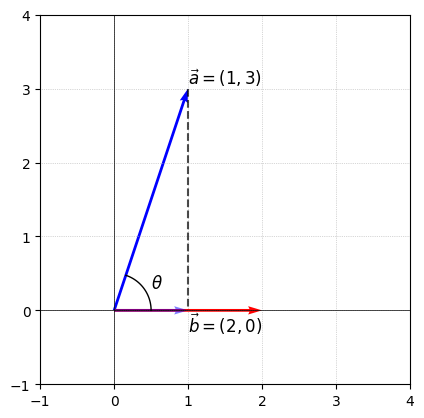
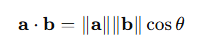
a와 b의 노름은 항상 양수이므로 코사인 값에 따라 양/음이 나뉜다
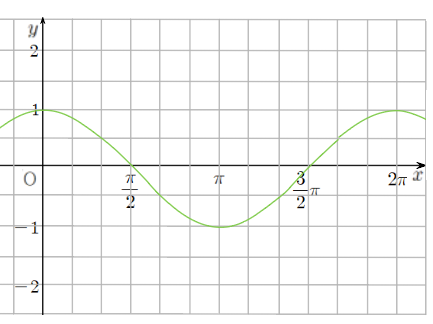
코사인 값 -1 ~ 1 사이
둘이 같은 방향일 때 1
둘이 반대 방향일 때 -1
직교일 때(90도) 코사인 값은 0
기하학적 내적 공식에 따라 직교 벡터의 내적은 0
-> 내적이 0이다 = 직교한다
내적(dot product): 두 벡터 사이의 관계를 숫자로 나타내는 것(유사성 척도로 사용)
벡터에 스칼라를 곱하면 내적도 그만큼 커진다
그러나 벡터의 크기가 크면 내적이 크게 나올 수 있으므로 정확한 유사성 판단이 불가하다
-> 정규화 해준다(벡터의 크기를 1로 만들어 벡터의 방향만 비교할 수 있게 한다)
내적의 분배 법칙
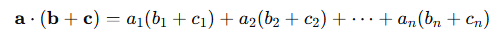
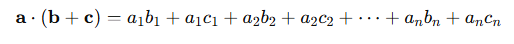
둘이 같기 때문에
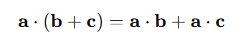
a = np.array([1,2,3])
b = np.array([4,5,6])
c = np.array([7,8,9])
print(np.dot(a, b+c))
print(np.dot(a,b) + np.dot(a,c))
내적의 교환 법칙
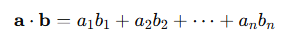
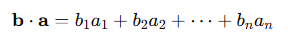
둘이 같기 때문에
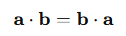
a = np.array([1,2,3])
b = np.array([4,5,6])
print(np.sum(a*b))
print(np.sum(b*a))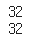
'혼자 공부 > 선형대수학' 카테고리의 다른 글
| 행렬의 연산, 행렬 곱의 전치 증명, 대칭 행렬 (0) | 2025.04.19 |
|---|---|
| 행렬1 (0) | 2025.04.17 |
| 상관관계와 코사인 유사도 (0) | 2025.03.18 |
| 벡터2 (0) | 2025.03.07 |
| 직교벡터 분해 (0) | 2025.03.05 |