행렬 (Matrix)
숫자들이 행과 열 형태로 정리된 표
성분 ( = 원소 = 항)
행렬 안에 배열된 구성값
Aij 는 A행렬의 i행 j열의 성분
행렬 A는 MXN행렬이라면
A는 M개의 행과 N개의 열로 이루어져 있다
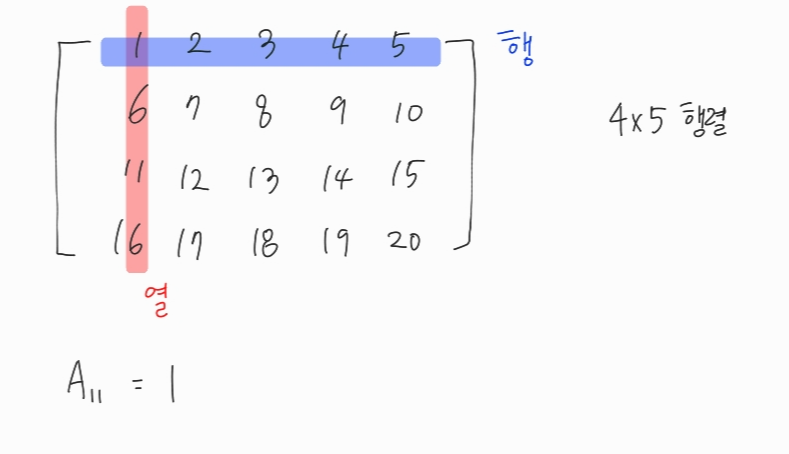
수학에서의 행렬과 파이썬에서의 행렬
수학은 1 기반 인덱싱
파이썬은 0 기반 인덱싱
넘파이를 이용한 행렬 만들기
import numpy as np
A = np.arange(1,21).reshape(4,-1) # 4행 5열 만들기

주대각선 (Main diagonal)
행렬의 왼쪽 위에서 오른쪽 아래를 가르는 선
대각 성분 (Diagonal elements)
주 대각선 위에 있는 성분들

전치 (Transpose)
행렬의 행과 열을 바꾼 행렬

넘파이를 이용한 전치
A.TA.transpose()


특수 행렬
1. 난수행렬(random numbers matrix)
정규 분포(가우시안 분포) 등에서 무작위 추출된 숫자들로 구성된 행렬
np.random.randn(row, column)
2. 정방행렬(square matrix)
행과 열의 수가 같은 행렬
+ 비정방행렬(nonsquare matrix): 행과 열의 수가 다른 행렬
3. 대각 행렬(diagonal matrix)
대각 성분을 제외한 나머지 원소는 모두 0
대각 성분은 0일 수도 있고 아닐 수도 있음
np.diag(행렬) # 대각 성분을 벡터로 반환
np.diag(벡터) # 벡터를 대각 성분로 한 행렬 반환
4. 삼각 행렬(triangular matrix)
주대각선을 기준으로 위/아래가 모두 0인 행렬
- 하삼각 행렬(lower triangular matrix)
대각선의 위가 모두 0

- 상삼각 행렬(upper triangular matrix)
대각선의 아래가 모두 0
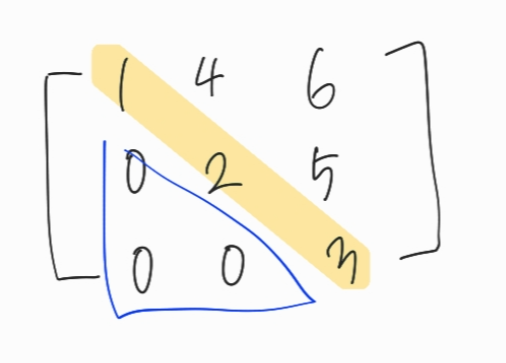
행렬을 하삼각행렬으로 만들기
np.till(matrix)
행렬을 상삼각행렬으로 만들기
np.tilu(matrix)

5. 단위 행렬 (Unit matrix) = 항등 행렬 (identity matrix)
기호: I 또는 U
대각 성분이 모두 1인 정방 대각 행렬(나머지 원소가 모두 0인 행렬)
np.eye(n)
행렬 a와 단위 행렬을 곱하면 항상 행렬 a가 나온다


6. 영 행렬(zero matrix)
기호: 0
모든 원소가 0인 행렬
np.zeros((row, column))
'혼자 공부 > 선형대수학' 카테고리의 다른 글
| 연립 일차 방정식 1 (0) | 2025.05.28 |
|---|---|
| 행렬의 연산, 행렬 곱의 전치 증명, 대칭 행렬 (0) | 2025.04.19 |
| 상관관계와 코사인 유사도 (0) | 2025.03.18 |
| 벡터2 (0) | 2025.03.07 |
| 직교벡터 분해 (0) | 2025.03.05 |