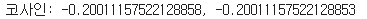상관관계와 코사인 유사도

https://product.kyobobook.co.kr/detail/S000209345747?utm_source=google&utm_medium=cpc&utm_campaign=googleSearch>_network=g>_keyword=>_target_id=aud-901091942354:dsa-608444978378>_campaign_id=9979905549>_adgroup_id=132556570510&gad_source=1

개발자를 위한 실전 선형대수학(파이썬 3.10 버전 대응, 구글 코랩 실습 가능) | 마이크 X 코헨 - 교

 

2025.03.03 - [혼자 공부/선형대수학] - 벡터1

벡터1

 

---

내적(dot product): 두 벡터 사이의 관계를 숫자로 나타내는 것(유사성 척도로 사용)

 

두 벡터의 유사성 판단 방법

1. 상관관계

2. 코사인 유사도

 

상관관계(correlation coefficient): 두 변수 사이의 선형 관계를 정량화한 수

 

그러나 벡터의 크기가 크면 내적이 크게 나올 수 있으므로 정확한 유사성 판단이 불가하다

-> 정규화 해준다(벡터의 크기를 1로 만들어 벡터의 방향만 비교할 수 있게 한다)

 

-1~1까지 (정규화 필요)
-1 음의 선형 관계 

0 아무 관계 없음

1 양의 선형 관계

상관관계가 0이더라도 비선형 관계는 존재할 수 있다

피어슨 상관계수 구하기

1. 평균 중심화(Mean Centering)

벡터에서 평균을 뺀다

2. 벡터 노름 곱으로 내적을 나눈다

 

노름으로 나누는 이유: 단위벡터(벡터의 방향은 유지하되 벡터의 크기를 1로 만든다)로 만들기 위해서.

단위벡터 만드는 공식

 

 

즉

 

 

코드를 이용한 피어슨 상관계수

import numpy as np
from scipy.stats import pearsonr

# 피어슨
def pearson(vec1, vec2):
  v1 = vec1 - np.mean(vec1)
  v2 = vec2 - np.mean(vec2)
  norm1 = np.sqrt(np.sum(v1**2))
  norm2 = np.sqrt(np.sum(v2**2))
  return np.sum(v1*v2) / (norm1*norm2)
  
v1 = np.random.randn(15)
v2 = np.random.randn(15)
print(f'피어슨: {pearson(v1, v2)}, \n\n{np.corrcoef(v1, v2)} \n\n{pearsonr(v1, v2)}')

 

+ 

그런데 표준편차가 위와 같으므로

표준화 공식이 된다.

-> 피어슨 상관계수는 각 데이터를 표준화한 후 그들의 내적을 계산한 값

 

https://angeloyeo.github.io/2019/08/20/correlation_and_inner_product.html

상관 계수와 벡터의 내적 - 공돌이의 수학정리노트 (Angelo's Math Notes)

 

 

 

코사인 유사도: 내적의 기하학적 공식을 이용

 

 

코드를 이용한 코사인 유사도

import numpy as np
from scipy.spatial.distance import cosine

def cosine_similarity(vec1, vec2):
  norm_vec1 = np.sqrt(np.sum(vec1**2))
  norm_vec2 = np.sqrt(np.sum(vec2**2))
  return np.sum(vec1*vec2) / (norm_vec1 * norm_vec2)

v1 = np.random.randn(15)
v2 = np.random.randn(15)

# cosine 함수는 거리(distance)를 반환하므로, 1에서 빼줘야 유사도가 됨
print(f'코사인: {cosine_similarity(v1, v2)}, {1-cosine(v1, v2)}')