개발자를 위한 실전 선형대수학(파이썬 3.10 버전 대응, 구글 코랩 실습 가능) | 마이크 X 코헨 - 교
개발자를 위한 실전 선형대수학(파이썬 3.10 버전 대응, 구글 코랩 실습 가능) | 복잡한 증명과 수식 없이 파이썬을 이용해 직관적으로 배우는 선형대수학 * 연습문제 + 해답 + 해설 강의, 무료 샘
product.kyobobook.co.kr
행렬의 덧셈과 뺄셈
크기가 같은 두 행렬 사이에서 같의 위치의 원소끼리 더하거나 뺀다
상수배
행렬의 각 원소에 상수 값을 곱한다.
행렬 아다마르곱
같은 위치의 원소끼리 곱한다.
matrix1 * matrix2
np.multiply(matrix1, matrix2)
표준 행렬 곱셈
일반적으로 행렬 곱이라고 하면 표준 행렬 곱셈을 뜻한다
왼쪽의 열과 오른쪽의 행 수가 같을 때 가능
m x n n x k = m x k
행렬의 (i,j)번 째 원소가 왼쪽 행렬의 i행과 오른쪽 행렬의 j열의 내적
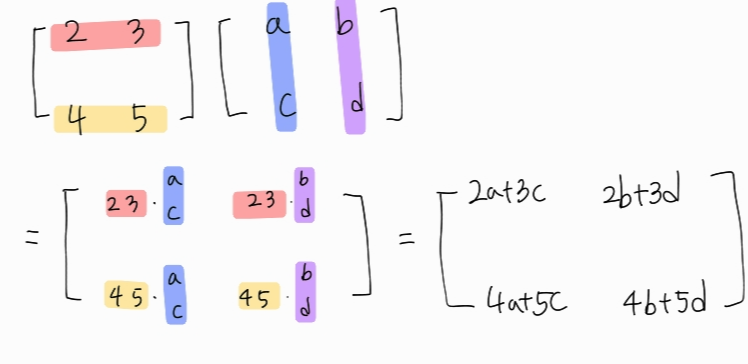
넘파이에서의 행렬 곱
matrix1 @ matrix2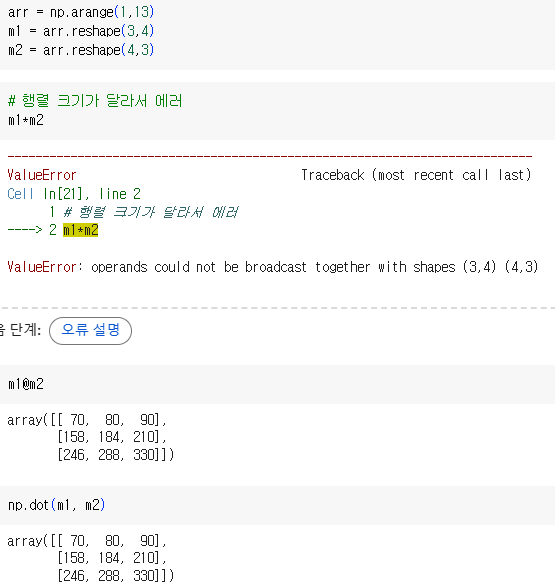
행렬 A, B가 있을 때
표준행렬곱셈은 교환 법칙 성립 안함
AB =/= BA
(BA가 유효하지 않을 수도 있음)

행렬-벡터 곱셈
행벡터 (1, m)의 shape
열벡터 (n,1)의 shape
행렬 (m,n)의 shape
행 벡터 x 행렬 -> 다른 행 벡터(m,1) 생성
행렬 x 열 벡터 -> 다른 열 벡터(1,n) 생성
-> 행렬-벡터 곱셈의 결과는 항상 벡터
넘파이로 열벡터 만들 때 대괄호의 수를 줄이기 위해 행벡터로 만든 다음 전치하기

+ 행렬-벡터 곱셈의 응용
1. 벡터의 선형 가중 결합을 구현하는 수단


2. 기하학적 변환을 구현하는 메커니즘
스칼라와 벡터 곱셈 -> 크기 조정 가능
행렬과 벡터 곱셈 -> 크기 조정과 회전도 가능
고유벡터를 곱하면 크기만 조정
행렬 곱의 전치
여러 행렬의 곱셈을 전치하면 개별 행렬을 전치하고 곱한 것과 동일하지만 순서는 뒤바뀐다
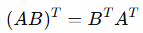
행렬 곱의 전치 공식 증명
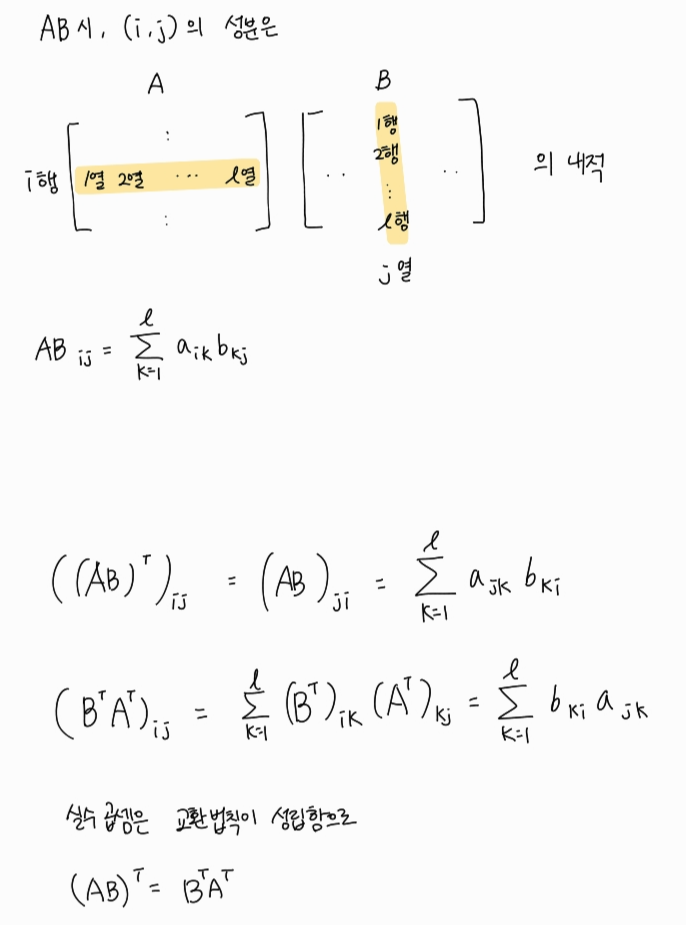
넘파이로 곱의 전치 공식 증명

대칭 행렬
행렬과 전치된 행렬이 같은 행렬(행과 열을 바꿔도 똑같은. 정방행렬이어야 가능)
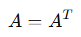
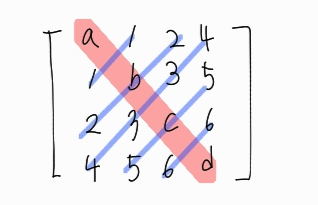
비정방행렬(M X N)은 전치를 했을 때 (N X M)이 나오기 때문에 대칭 행렬이 될 수가 없다.
비대칭 행렬(M X N) -> 대칭 행렬 만드는 법(M X M)
자신의 전치행렬을 곱하면 대칭 행렬이 됨
-> 모든 행렬에 자신의 전치 행렬을 곱하면 대칭 행렬을 만들 수 있다 (특잇값 분해의 핵심)
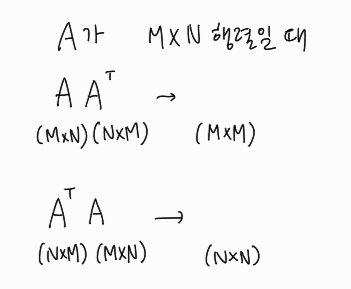
증명(행렬 곱의 전치 공식 사용)

행렬 곱의 전치 증명 참고
https://m.blog.naver.com/crm06217/221655332464
[선형대수학(증명) - 1] 기본적인 행렬 및 행렬 연산(역행렬, 전치행렬 등)
선형대수학은 증명이 많다. 그래서 추상적으로 느껴지기도 한다. 뻔한 말이지만 수학은 정의에서 출발한다....
blog.naver.com
https://plusthemath.tistory.com/454
[더플러스수학] (AB)^T=B^T A^T 증명 (전치행렬의 성질)
\(\displaystyle (AB)^T =B^T A^T \)을 증명해보자. 먼저 행렬 \(\displaystyle A\)를 \(\displaystyle l \times m \)행렬, 행렬 \(\displaystyle B \)를 \(\displaystyle m \times n \) 행렬이라 하자. 행렬 \(\displaystyle AB\)는 \(\displaystyl
plusthemath.tistory.com
'혼자 공부 > 선형대수학' 카테고리의 다른 글
| 연립 일차 방정식 1 (0) | 2025.05.28 |
|---|---|
| 행렬1 (0) | 2025.04.17 |
| 상관관계와 코사인 유사도 (0) | 2025.03.18 |
| 벡터2 (0) | 2025.03.07 |
| 직교벡터 분해 (0) | 2025.03.05 |