클러스터링
좀 더 의미있는 인사이트를 추출하기 위해 유사한 데이터들을 클러스터(집단)으로 묶어주는 것
비지도학습 중 하나(정답이 주어지지 않은 상태에서 스스로 찾아내는 것)
정답을 주지 않아도, 알아서 클러스터를 나눠준다
하지만 해당 클러스터가 무엇을 의미하는지는 분석해주지 않는다
-유사한 데이터는 같은 클러스터로 묶는다
-유사하지 않은 데이터는 다른 클러스터로 묶는다
유사의 기준
1. 거리
2. 계층
3. 밀도
4. 분포
1. 거리 기반 클러스터링(K-Means)
k개의 중심점을 임의로 배치한 후 각 중심점과 가까이 있는 데이터들을 클러스터로 묶어주고, 중심점을 클러스터 내 데이터들의 중심으로 이동시킨다 -> 중심점 위치 갱신 안할 때까지 반복
필요 라이브러리 임포트
from sklearn.cluster import KMeans
#시각화
import seaborn as sns
모델 선언 및 학습
model = KMeans(n_clusters=k, random_state=2023)
model.fit(df)KMeans의 파라미터
n_clusters : 나눠질 군집 개수 k
random_state : 여러 번 모델을 학습시켜도 동일한 결과가 나오도록 해줌
클러스터 구분 컬럼 추가
df['cluster'] = model.predict(df)
#클러스터 당 개수 세기
df['cluster'].value_counts()model.predict()를 사용한다
각 군집의 중심점
centers = model.cluster_centers_
centers를 보면
array([[-0.56465473, -0.60996397],
[ 0.9478133 , 1.02386809]])x, y축의 좌표 형태로 나온다(k를 2로 해서 2개가 나온 것)
최적의 k 값 선정 기준
군집의 데이터들과 각 군집의 중심점과의 거리를 제곱하여 더한 값
#이너시아
model.inertia_
Elbow Method
k가 1~15일 때까지 이너시아 시각화
inertia = []
#k는 1~15까지
for k in range(1,16):
model = KMeans(n_clusters = k, random_state = 2023)
model.fit(df)
inertia.append(model.inertia_)
sns.lineplot(x=range(1, 16), y=inertia, marker='o')

분석하기 좋은 것으로 k를 선택한다
클러스터링 시각화
seaborn 라이브러리 임포트
sns.scatterplot(x='컬럼1', y='컬럼2', hue='cluster')
#방법1
sns.scatterplot(x=df['컬럼1'], y=df['컬럼2'], hue=df['cluster'])
#방법2
sns.scatterplot(x='컬럼1', y=df'컬럼2', hue='cluster', data=df)
Seaborn을 이용한 시각화
matplotlib이 기반인 시각화 패키지로, 다양한 색상 사용과 차트 기능이 존재한다.
velog.io
+ 스케일링
정규화나 표준화를 하여 데이터를 스케일링 하면 실제 분석에서 특성을 알아내기 어렵기 때문에
클러스터링을 할 때만 스케일링 하고, 실제 분석에서는 원본 데이터를 사용한다
KMeans의 단점
1. k를 미리 정해야 하는데, 정하기 어렵다
2. 이상치에 영향을 많이 받는다 -> 이상치 제거 / 다른 모델 사용
3. 초기에 군집의 중심점인 centroid의 영향을 받아, 모델 시간이 오래 걸릴 수 있다 -> init = 'k-means++' 사용
from sklearn.cluster import KMeans
model = KMeans(n_clusters=k, init='k-means++')4. 차원이 높은 데이터에 성능이 떨어진다
즉 변수가 많아질수록 차원이 높아지고, 차원이 높아지면 데이터 간의 거리가 멀어지고, 유사한 군집으로 묶는 정확성이 떨어진다
차원의 저주
https://www.codeit.kr/community/questions/UXVlc3Rpb246NjQ4ZWRkYWNmZGE1NmUxM2JkM2Y4YjNi
K means 에서 몇차원 이하로 해야 차원의 저주에 빠지지 않나요?
www.codeit.kr
2. 계층적 클러스터링
각 데이터 사이의 거리를 모두 계산하여 가장 가까운 데이터 쌍을 차례대로 묶고, 묶인 데이터 쌍 끼리도 거리를 계산하여, 가까운 쌍은 하나로 묶는다 -> 다 묶을 때까지 반복
계층적 클러스터링의 특징
개수를 미리 정하지 않고 클러스터링이 가능하다
거리 계산을 위해 많은 연산이 필요하여 대용량 데이터에는 힘들다
필요 라이브러리 임포트(scipy 사용)
from scipy.cluster.hierarchy import dendrogram, linkage, cut_tree
#시각화
import matplotlib.pyplot as plt
import seaborn as snslinkage: fit
cut_tree: predict
dendrogram: 시각화
ward 거리를 이용하여 모델 선언 및 학습
# 거리 : ward method
model = linkage(df, 'ward')
덴드로그램을 이용하여 시각화
dendrogram(model, labels=df.index)
plt.show()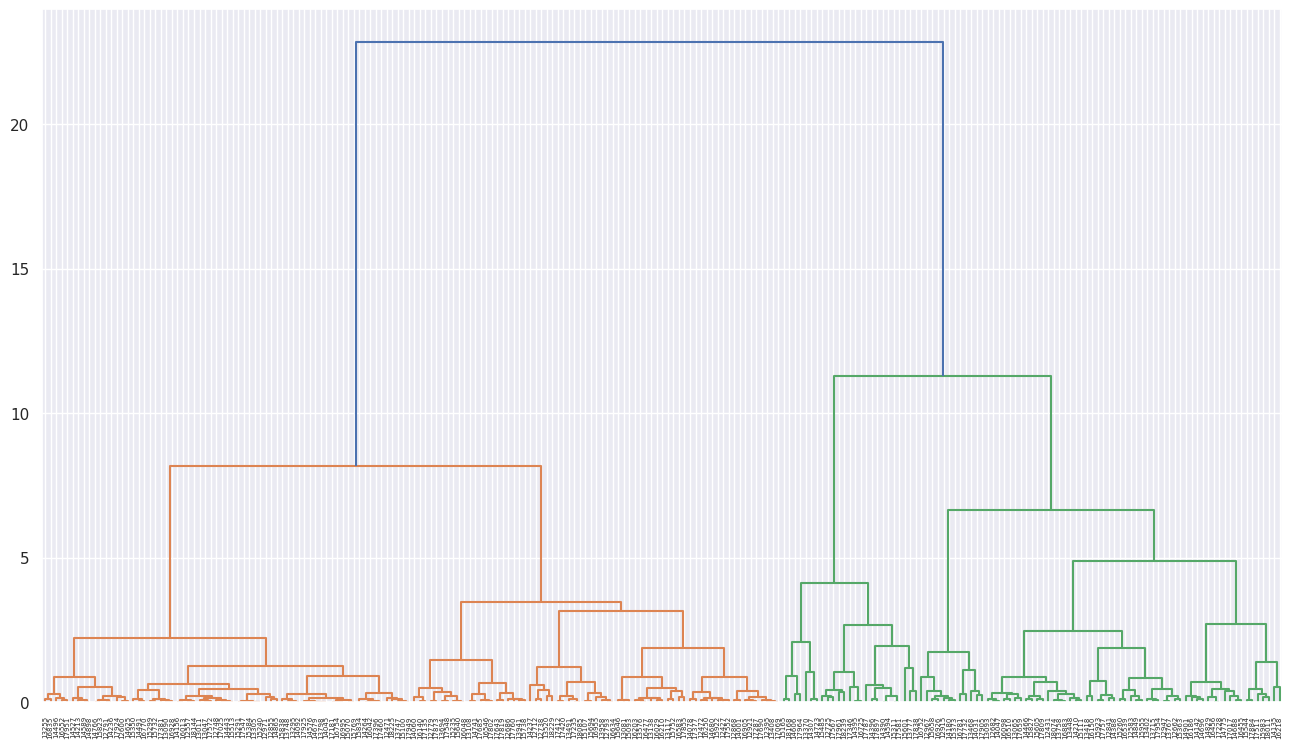
클러스터 구분 컬럼 추가
#클러스터 수를 5로 지정
cluster_num = 5
df['cluster'] = cut_tree(model, cluster_num)
df['cluster'].value_counts()
시각화는 위와 똑같다
3. 밀도 기반 클러스터링(DBSCAN)
반경과 최소 데이터 개수를 정해서 사용한다
각 클러스터의 반경이 곂치면 두 클러스터를 하나로 묶는다
어떤 클러스터에도 포함되지 못하면 이상치가 된다(이상치에 강함)
필요 라이브러리 임포트
from sklearn.cluster import DBSCAN
#시각화
import seaborn as sns
모델 선언 및 학습
model = DBSCAN(eps=반경 값, min_samples=최소 데이터 개수)
model.fit(df)
클러스터 구분 컬럼 추가
df['cluster'] = model.labels_
df['cluster'].value_counts()model.predict()가 아닌 model.labels_를 사용한다
시각화는 위와 똑같다
4. 분포 기반 클러스터링(GMM)
데이터가 정규 분포를 따를 때 특정 데이터의 값이 어떤 분포에 포함될 확률을 보고 확률이 높은 클러스터로 구분해준다
GMM 특징
분포 개수를 미리 설정해야 한다
특정 분포에 데이터 수가 충분히 있어야 한다
정규 분포를 가정하기 때문에 범주형 데이터에는 불가능하다
필요 라이브러리 임포트
from sklearn.mixture import GaussianMixture
import seaborn as sns
모델 선언 및 학습
model = GaussianMixture(n_components=분포 개수, random_state=2023)
model.fit(df)
클러스터 구분 컬럼 추가
df['cluster'] = model.predict(df)
df['cluster'].value_counts()
시각화는 위와 똑같다
'빅데이터 공부' 카테고리의 다른 글
| PCA (2) | 2024.01.09 |
|---|---|
| [빅데이터분석기사 실기] 제3유형-가설검정 (0) | 2024.01.08 |
| [빅데이터분석기사 실기] 제2유형 (1) | 2023.12.18 |
| 데이터 클리닝 (0) | 2023.11.29 |
| 판다스 기본 제공 메소드로 시각화하기 (2) | 2023.11.23 |