배낭 문제라고도 불리는 냅색 알고리즘은 DP 문제 중 일부이다.
주어진 물건들 중 일부를 선택하여 제한된 용량의 가방(또는 배낭)에 최대한의 가치를 담는 문제를 해결하는 알고리즘
물건을 넣을 것인가, 안넣을 것인가를 정하는 것이 문제의 핵심이다.
평범한 배낭 문제를 이용하여 원리를 알아보겠다

https://www.acmicpc.net/problem/12865
일단 예제 1을 보면
4 7 # 물품 수 n 과 최대 무게 k
# 각 물품의 무게와 가치
6 13
4 8
3 6
5 12
물품 수 n+1 (아무 물품도 넣지 않았을 때)를 행으로
무게 k+1 (무게가 0일 때)를 열로 한
2차원 표를 만든다

2차원 표 안에는 가치가 들어간다.
각 행의 물건을 넣었을 때, 넣지 않았을 때의 가치를 비교해서 더 큰 값을 넣어준다
안넣는 경우
- 물건의 무게보다 수용할 수 있는 무게가 작을 때
- 안 넣었을 때 가치가 더 큰 경우
일단 물품이 없을 때, 무게가 0일 때는 모두 가치가 없기 때문에 0으로 초기화해준다.

이제 무게 6, 가치 13 짜리 물건을 넣을 지 말지, 고민해본다.

1 만큼의 무게만 수용할 수 있기 때문에, 물건을 넣지 못하고, 위의 행의 값을 가져온다
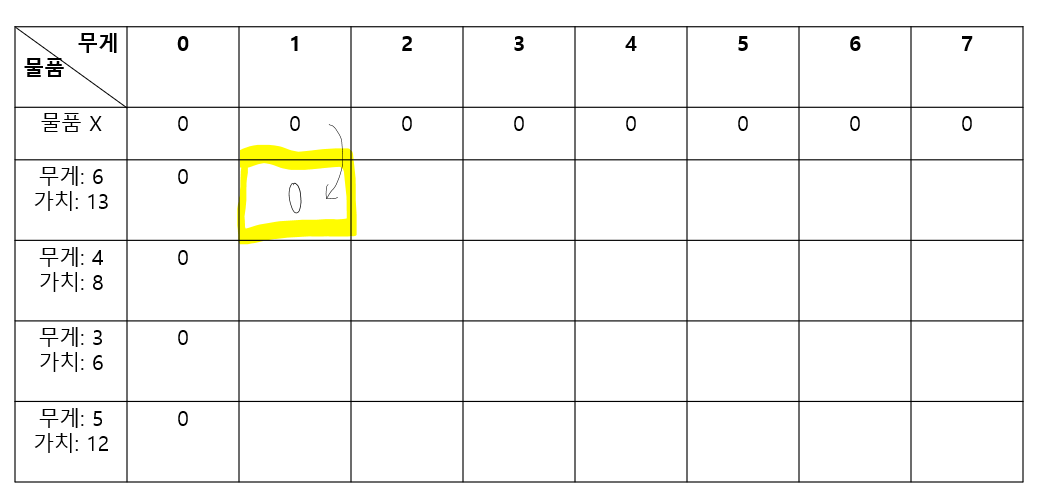
그러면 6을 수용할 수 있는 가방이 나올 때까지는 물건을 넣을 수 없다
그렇다면 6을 수용할 수 있을 때를 살펴본다
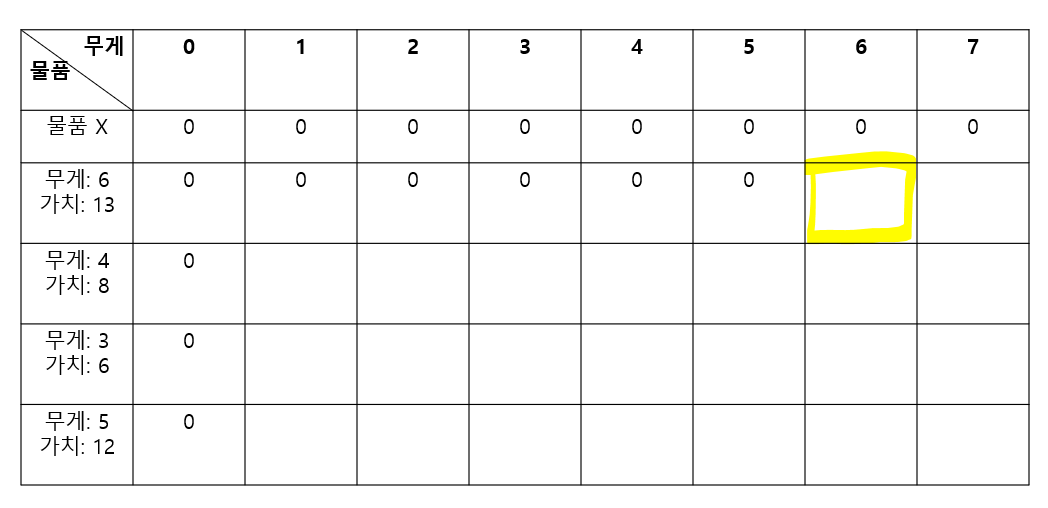
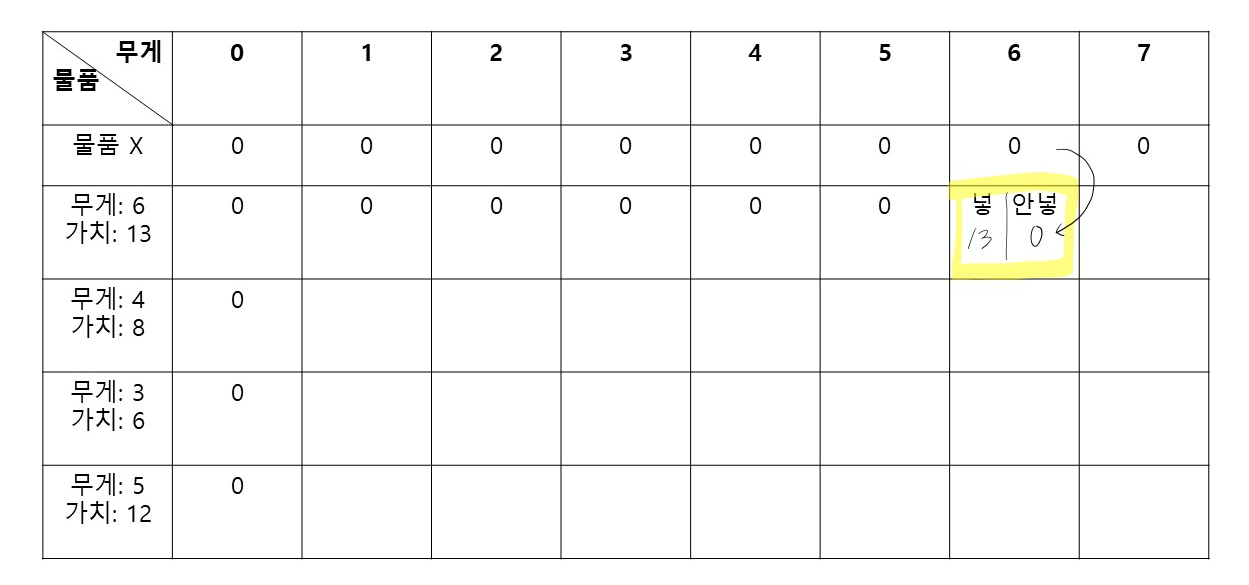
6만큼을 수용하는 가방에
6짜리 물건을
안 넣을 때는 0의 가치,
넣을 때는 13의 가치를 얻을 수 있다
7만큼을 수용하는 가방에
6짜리 물건을
안 넣을 때는 0의 가치가 나온다.
넣을 때는 6짜리 물건을 넣고도, 1만큼을 더 수용할 수 있기 때문에 13 + 물품X의 1짜리만큼 넣을 수 있다
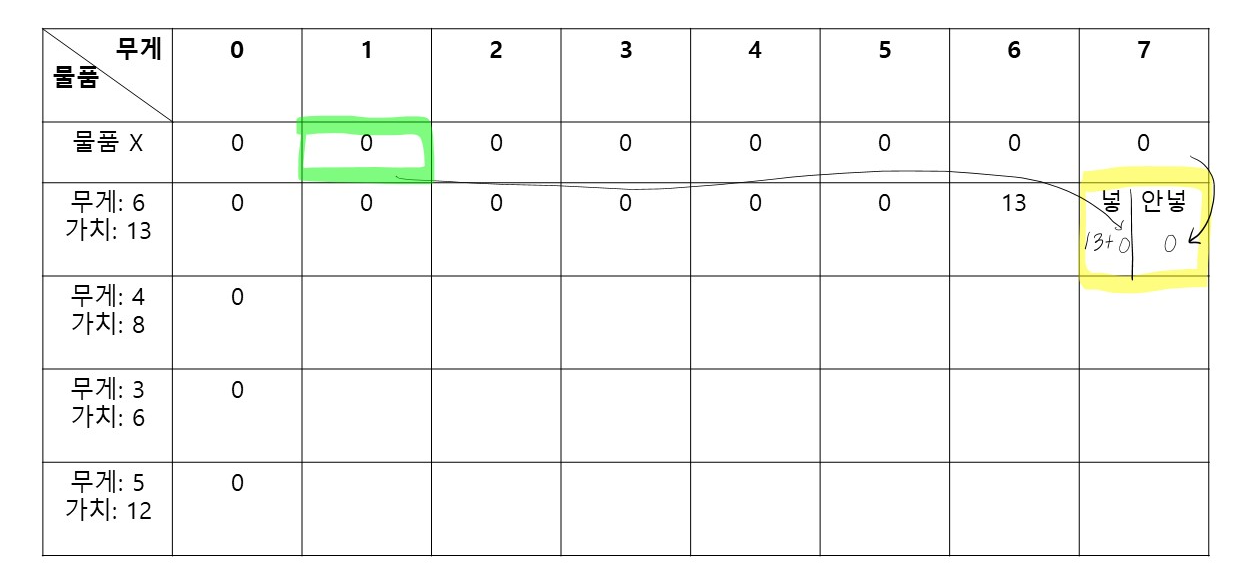
이렇게 쭉 반복한다.
이번에는
7만큼을 수용하는 가방에
3짜리 물건을 넣을지 말지 알아보겠다.
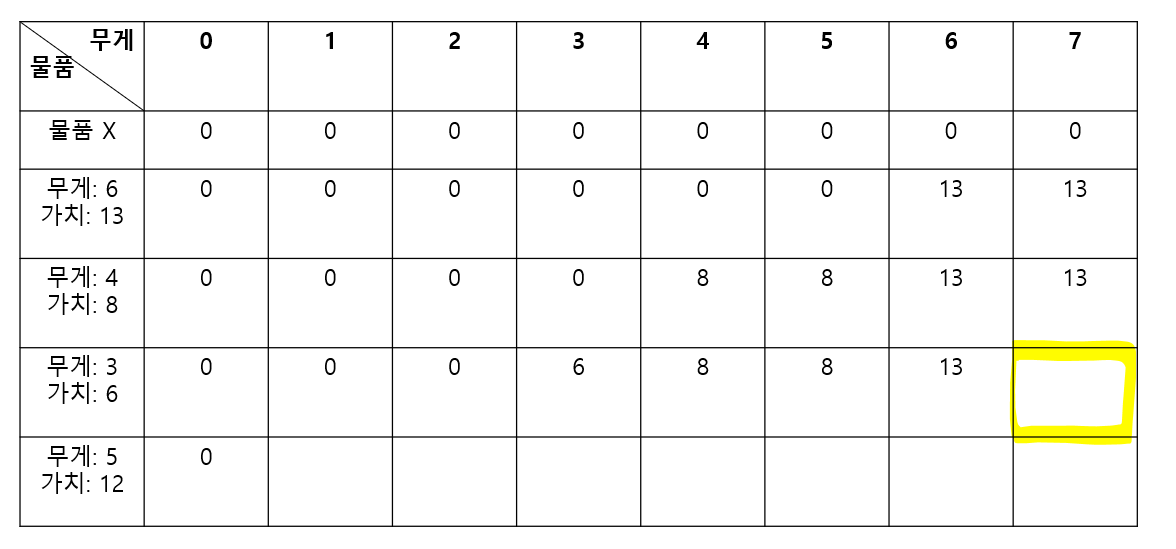
안 넣을 때는 13의 가치가 나온다.
넣을 때는 3짜리 물건을 넣고도, 4만큼을 더 수용할 수 있기 때문에 무게 4인 물건을 더 넣을 수 있다
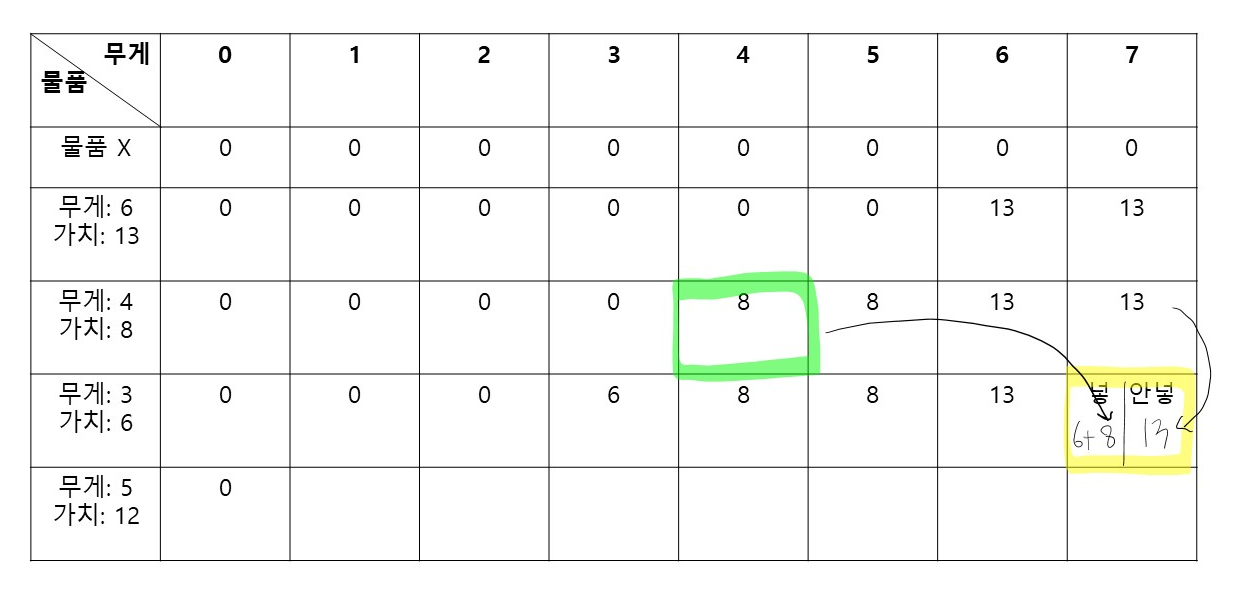
그렇게 해서 최대로 14의 값을 넣을 수 있다
표를 완성시키면,
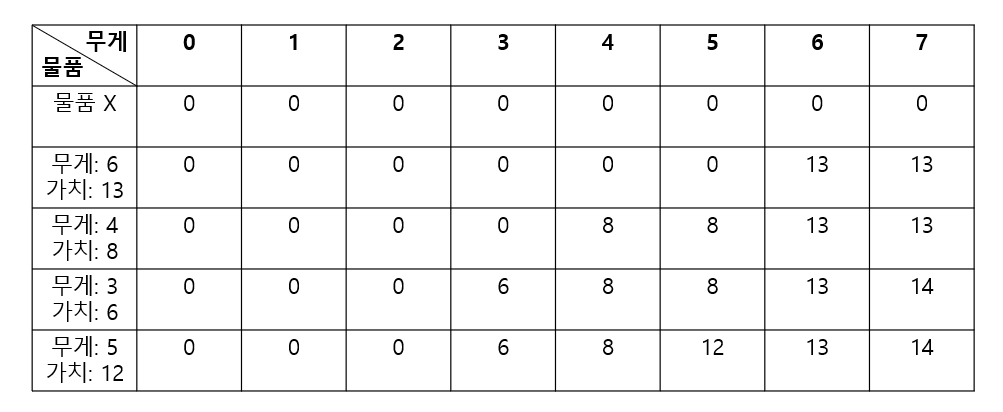
이제 지금까지의 것을 점화식으로 만들어보겠다
dp를 2차원 리스트로 정의하면
dp = [[0] * (k+1) for _ in range(n+1)]
# nn번 째 물건, kk 무게까지 수용하는 가방
# value[nn]은 nn의 가치
# weight[nn]은 nn의 무게
dp[nn][kk] = max(dp[nn - 1][kk], value[nn] + dp[nn - 1][kk - weight[nn]]) # 안 넣었을 때, 넣었을 때
평범한 배낭 문제를 푼다면
import sys
input = sys.stdin.readline
n, k = map(int, input().split())
wv = [[]]
for _ in range(n):
w, v= map(int, input().split())
wv.append((w,v))
# 냅색 점화식
# ns(n, w) = max(ns(n-1, w), ns(n-1, w-wv[i][0])+wv[i][1])
# 행: 들어가는 가방 수
# 열: 무게 수
dp = [[0]*(k+1) for _ in range(n+1)]
for i in range(1, n+1):
w, v = wv[i]
for j in range(1, k+1):
if w > j:
dp[i][j] = dp[i-1][j]
else:
dp[i][j] = max(dp[i-1][j], dp[i-1][j-w] +v) # 지금 가방 안들었을 때, 지금 가방 들었을 때
print(dp[n][k])가 된다.